数据结构复习-第二部分

本系列文章为作者复习数据结构过程中的知识点总结、速通，欢迎补充

Written by SJTU-XHW

Reference: 张同珍老师 PPT | UNIkeEN

注：默认定义异常类型noElementException：

class noElementException {
private:
    const char* message;
public:
    noElementException(const char* msg="No element in the container.")
        : message(msg) {}
    const char* what() const { return message; }
};

Chapter 3 栈

3.1 零碎概念集合

栈的地位：一种特殊的（后进先出，LIFO）的线性表，仅允许在一端插入、同一端删除；

栈底、栈顶、空栈、进栈/压栈、出栈/弹栈的定义；
栈的基本运算：创、进出、读头、判空；
时间有序表：因为栈的元素关系和离开、到达的时间有关，所以栈又被称为时间有序表

3.2 栈的顺序实现

存储实现：数组模拟栈，idx=0为栈底；【数组头指针、规模数、栈顶位置】

注意：栈顶位置数的地方存放有效数据，所以空栈的栈顶位置习惯为-1；

运算实现：过于简单，一笔带过

template <class T>
class seqStack {
private:
    T* data;
    int maxSize;
    int topIdx;
    
    void doubleSpace() {
        T* tmp = data;
        data = new T[maxSize * 2];
        for (int i = 0; i <= topIdx; ++i)
            data[i] = tmp[i];
        delete[] tmp; maxSize *= 2;
    }
public:
    seqStack(int capacity=10) {
        data = new T[capacity];
        maxSize = capacity; topIdx = -1;
    }
    ~seqStack() { if (data) delete[] data; }
    bool isempty() const { return topIdx == -1; }
    
    // 时间复杂度均摊分析：平均 O(1)
    void push(const T& dt) {
        if (topIdx == maxSize - 1) doubleSpace();
        data[++topIdx] = dt;
    }
    T pop() {
        if (topIdx == -1) throw noElementException();
        return data[topIdx--];
    }
    T top() const {
        if (topIdx == -1) throw noElementException();
        return data[topIdx];
    }
};

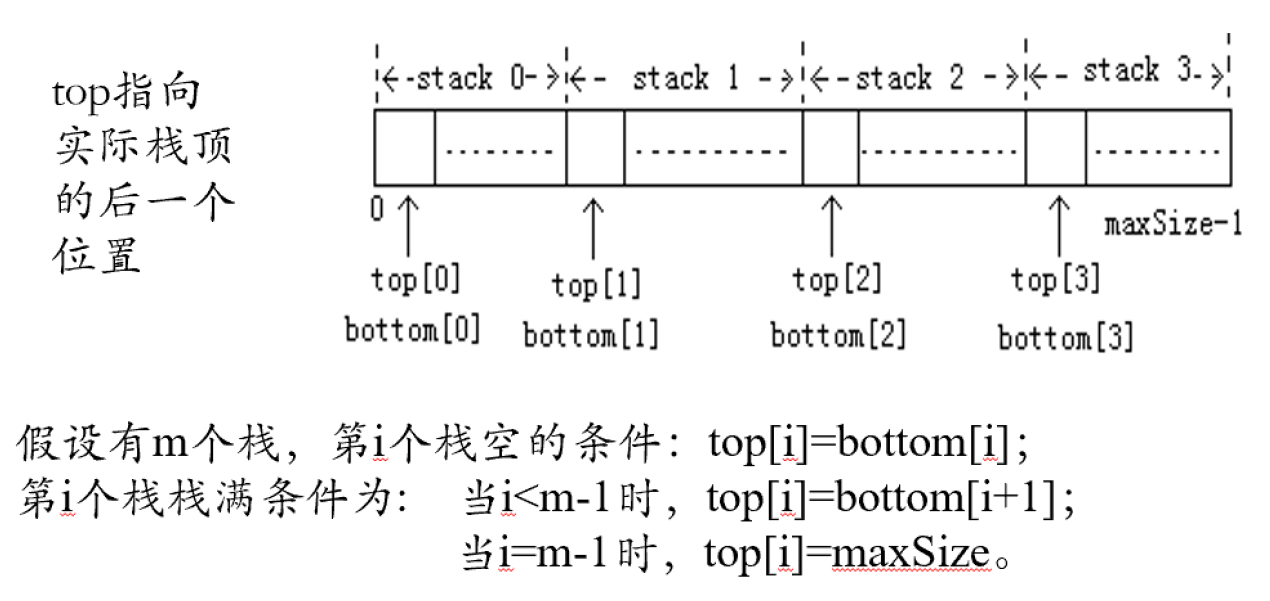
3.3 顺序栈的变种：共享栈

为了提高空间利用率，在某些实际问题中使用多个数据类型相同的栈时，在一块连续的空间中设置多个栈共享空间，其中每个栈有连续的小空间，如图所示。

提示：对栈操作的函数会添加一个整型参数指定究竟对谁操作

3.4 栈的链接实现

存储实现：所有操作在栈顶完成——无需头结点的单链表；【栈顶指针】

运算实现：解说略；

template <class T>
class linkStack {
private:
    struct node {
        T data;
        node* next;
        node() { next = 0; }
        node(const T& dt, node* n=0)
            : data(dt), next(n) {}
    };
    node* top;
public:
    linkStack() { top = nullptr; }
    ~linkStack() {
        while (top) {
            node* tmp = top;
            top = top->next;
            delete[] tmp;
        }
    }
    bool isempty() const { return top == nullptr; }
    void push(const T& dt) {
        top = new node<T>(dt, top);
    }
    T pop() {
        if (top == nullptr) throw noElementException();
        T ans = top->data;
        node* tmp = top;
        top = top->next; delete tmp;
    }
    T getTop() const {
        if (top == nullptr) throw noElementException();
        return top->data;
    }
};

3.5 栈的应用

判断回文序列

手动消除递归

经典例题：Ackerman 函数非递归求解、非递归快速排序

$\begin{aligned} &已知Ackerman函数的定义(m、n均为非负整数):\\ &A(m,n)=\begin{equation}\left\{\begin{aligned}&n+1\qquad&if\space m=0\\&A(m-1,1)\quad&if\space m\gt0\space and\space n=0\\&A(m-1,A(m,n-1))&if\space m\gt0\space and\space n\gt0\\\end{aligned}\right.\end{equation}\\ &\\ &试用非递归方法定义Ackerman计算函数:\\ \end{aligned}$

1	int Ackerman(int m, int n); // 允许使用 seqStack 类

具体思路：定义栈中的元素类型为保存m、n两个数的结构体（可以使用C++内置STL pair），先将A(m, n)作为一个元素放入栈中开始循环，循环判断栈非空进入，每次弹出一个元素计算。

如果 m > 0 且 n = 0，那么构建新的元素A(m-1, 1)放进栈中；

如果 m > 0 且 n > 0，那么不妨把用不到的负数 -1 作为未计算的结果代替 A(m, n-1)，构建元素A(m-1, -1)进栈，紧接着进栈A(m, n-1)来补充前面的-1的含义，等待计算；

如果直接计算出结果（m=0），那么检查栈是否为空，如果空，说明计算完成，结束；如果非空，那么说明这个结果一定是前一个被-1代替的位置上的结果，只需再弹出一个元素，将其中-1改为当前结果再进栈即可；
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
int Ackerman(int m, int n) {
 struct node {
     int m, n;
     node(int m_=-1,int n_=-1)
         :m(m_), n(n_) {}
 };
 seqStack<node> stk;
 stk.push(node(m, n));
 while (!stk.isempty()) {
     node tmp = stk.pop();
     if (tmp.m == 0) {
         if (stk.isempty())
             return tmp.n + 1;
         else {
             node pre = stk.pop();
             stk.push(node(pre.m, tmp.n+1));
         }
     }
     else if (tmp.n == 0)
         stk.push(node(tmp.m-1, 1));
     else {
         stk.push(node(tmp.m-1, -1));
         stk.push(node(tmp.m, tmp.n-1));
     }
 }
}

括号匹配

思路：读入开括号进栈，读入闭括号检查（如果空栈，错误；如果非空则弹出，弹出再检查，如果不匹配则有错误）；最后读取结束必须空栈，否则错误；

表达式计算

前缀表达式、中缀表达式、后缀表达式的定义；

中缀表达式转后缀表达式

// 从左至右读取中缀表达式
while (当前字符非空) {
    if (读入操作数) 直接输出到后缀表达式中
    if (读入开括号) 直接进运算符栈
    // 括号内的运算符优先级优先于括号外
    if (读入闭括号) 栈内运算符依此弹出并输出，直至开括号停止
    if (读入操作符) {
        // 最高运算符优先级，右结合
        if (操作符是 ^ ) 直接进栈
        // 之前同级、或更高级的运算符可以优先运算
        if (操作符是 */ ) 可以一直出栈，直至遇到 +-或左括号或空，自己进栈
        if (操作符是 +- ) 可以一直出栈，直至遇到左括号或空，自己进栈
    }
}
while (栈非空) {
    运算符出栈，输出到后缀表达式中
    if (出栈元素有括号)
        报告表达式错误
}

后缀表达式的计算

// 从左至右读取后缀表达式
while (当前字符非空) {
    if (读入操作数) 进操作数栈
    if (读到运算符) 将指定元数的操作数依此（后出被运算数）出栈进行运算，结果进栈
}
结果出栈
if (栈非空)
    报告表达式错误

Chapter 4 队列

4.1 零碎概念集合

队列的地位：一种特殊的、先进先出（FIFO）的线性表；允许在一端插入、另一端删除；
1. 队尾与队头、队列长度、空队列、入队和出队的定义；
2. 队列也是一种时间有序表；
队列的基本运算种类：创建、读头、判空、入队、出队；

4.2 队列的顺序实现

和栈不同，如何设计队头、队尾对性能影响极大；

↪ 队首位置固定方式，缺点是出队会引起大量数据移动

↪ 队首位置不固定方式，所有操作都是O（1），但浪费空间。

最好的一种存储实现之一：循环队列【队头整型、队尾整型、顺序表头指针、规模数】
- 队头指针（int）区域不存放数据，队尾指针在非空是总是指向最后一个数；
- 可以使用取余的方法将队列的空间充分利用；

运算实现：解说略

template <class T>
class seqQueue {
private:
    int head;
    int tail;
    T* data;
    int maxSize;
    
    void doubleSpace() {
        T* tmp = data;
        data = new T[2 * maxSize];
        for (int i = 1; i < maxSize; ++i) {
            data[i] = tmp[(head + i) % maxSize];
        }
        delete[] tmp;
        head = 0; tail = maxSize; maxSize *= 2;
    }
public:
    seqQueue(int capacity=10) {
        maxSize = capacity;
        data = new T[capacity];
        head = tail = -1;
    }
    ~seqQueue() { if (data) delete[] data; }
       bool isempty() const { return head == tail; }
    T getHead() const { 
        if (head == tail) throw noElementException();
        return data[(head + 1) % maxSize];
    }
    void enQueue(const T& dt) {
        if ((tail + 1) % maxSize == head)
            doubleSpace();
        tail = (tail + 1) % maxSize;
        data[tail] = dt;
    }
    T deQueue() {
        if (head == tail) throw noElementException();
        head = (head + 1) % maxSize;
        return data[head];
    }
};

易错点：doubleSpace时将顺序表扩大时注意0索引区域不放数据！

4.3 队列的链接实现

法一：使用无头结点的单链表存储队列—->【队头、队尾指针】

法二：使用单循环链表—->【队尾指针】

4.4 队列的实际应用

排队系统模拟：事件驱动模拟
火车车厢重排
迷宫矩阵问题
- 寻找可能解【DFS】：栈消除递归进行回溯；
- 寻找最优解【BFS】：利用队列同步检查所有可能道路，先到终点的连通道路就是最短道路

Chapter 5 二叉树、树和森林

5.1 重要概念集合

树的两种定义
1. 在一个元素集合中，如果元素呈上下层次关系。对一个结点而言，上层元素为其直接前驱且直接前驱唯一，下层元素为其直接后继且直接后继可以有多个，这样的结构就是树结构。
2. 递归定义：树是n个结点（离散数学要求n > 0）的有限集合，它或者是空集，或者满足：
  - 有一个被称为根的结点；
  - 其余结点可分为m（m > 0）个互不相交的集合 T1, T2, ..., Tm这些集合本身也是一棵树，并称它们为根结点的子树；
各类结点的定义
- 根结点、叶结点、内部节点/中间结点；
- 子结点、父结点、祖先结点、子孙结点、兄弟结点；
  
  注意：兄弟结点只有同一父结点才算！！！否则叫堂兄弟结点；
各种“度”
- 结点的度：树中一个结点的直接后继（子结点）的数目；
- 结点深度（层次）：从根结点（高度定为1）向下到该结点的对应数；
- 结点高度：以该结点为根的子树的高度；
- 树的高度：树中所有结点的最大深度；
有序树和无序树：如果树中任意结点的子结点都被规定了一定的顺序，就称此树为有序树，反之称为无序树；
森林：M棵互不相交的树的集合

由定义，一棵删去根的树，其子树构成的集合就是一个森林；

5.2 二叉树的重要概念

定义：建议将树的定义代入，只需注意二叉的特点；

注意：二叉树的子结点需要明确指明是左还是右，哪怕只有一个子结点
特殊二叉树
- 满二叉树：k层二叉树的每一个结点数量都达最大值；
- 完全二叉树：k层二叉树的k-1层都是满的，k层相较于满二叉树从右至左依此去掉若干结点得到的树；
二叉树性质
- 一棵非空二叉树的第 i 层上最多有 $2^{i-1}$ 个结点（i ≥ 1）；
- 一棵高度为 k 的二叉树最多有 $2^k-1$ 个结点；
- 一棵非空二叉树，若叶结点数 $n_0$，度为 2 的结点数 $n_2$，则 $n_0=n_2+1$；
- 具有 n 个结点的完全二叉树的高度一定为 $k=floor(log_2n)+1$
- 对有 n 个结点的完全二叉树的结点按层自上而下，每一层自左至右依此编号，设根结点编号为 1，那么：
  $\begin{aligned} &1.\quad i=1\Longleftrightarrow 该二叉树根结点;\quad i\gt 1\Longrightarrow 该结点的父结点编号floor(\dfrac{i}{2})\\ &2.\quad 若\space 2i\gt n,\space则编号为\space i\space的结点为叶结点,否则其左子结点编号为\space 2i\\ &3.\quad若\space2i+1\gt n,\space 则编号为\space i\space的结点没有右子结点，否则其右子结点的编号为\space 2i+1 \end{aligned}$
二叉树的基本运算：创清、判空、寻根、寻父、寻左儿子寻右儿子、删左儿子删右儿子、遍历
二叉树的遍历序列和确定
- 二叉树的前序-中序、后序-中序、层次-中序遍历序列都可以确定唯一一个二叉树（必须含有中序）
- 完全二叉树的层次遍历能唯一确定该完全二叉树；
- 满二叉树的前序、中序、后序遍历序列之一就能完全确定该满二叉树；
- 做题方法：遇到从某些序列构建完整的二叉树时，应该在过程中反复比对
考题分析
- 一个完全二叉树的叶结点个数为124，问该树所有结点的最大个数为多少；
  分析方法一：完全二叉树的叶结点为124，先考虑满二叉树的情况（注意到在所有的、高度相同的完全二叉树中，满二叉树的叶结点最大！），满二叉树高度为7时，64个叶结点；满二叉树高度为8时，128个叶结点；满二叉树高度为9时，256个叶结点，且倒数第二层共128个内部结点；因此：
  - 该树的高度一定大于7、小于9 $\Longrightarrow$ 该树的高度为8；
  再考虑从满二叉树减少结点，每减少两个兄弟结点中的一个，叶结点数减少1（只剩一个时不会变）；所以满足条件的完全二叉树可以：从8层满二叉树下自右至左减去 8 个或 7 个叶结点，即 $n_{max}=2^8-1-7=248$
  
  分析方法二（最优解）：
  
  由于完全二叉树必须有：$n_1=1或0$，故 $n_{max}=124+1+123=248$
  
  结论：该树的所有节点最大个数为 248

5.3 二叉树的存储和运算实现

顺序实现：仅建议完全二叉树 / 具有一些结点关系的树（例如哈夫曼树）/ 不需要频繁增删结点的普通二叉树采用这种存储方式，否则导致空间利用率低下；

[x] 二叉树的主要存储方式是链接实现的

标准存储结构（最常用）：二叉链表【表头指针】
- 大多数操作简单，但寻父运算性能不佳；
广义标准存储结构：三叉链表【表头指针】

二叉树运算实现

寻左右儿子、删左右儿子的函数需要底层的find函数先查找；
清除、删左右儿子的函数需要底层的“删除结点及其子树”的clear函数；
深度优先的递归的消除采用栈，广度优先采用队列实现；

下面以非递归实现的标准存储的二叉树为例

template <class T>
class binTree {
private:
    struct node {
        T data;
        node* left;
        node* right;
        node(): left(0), right(0) {}
        node(const T& dt, node* L=0, node* R=0)
            : data(dt), left(L), right(R) {}
    };
    struct travNode {
        node* curNode;
        int popTimes;
        travNode(node* n=0, int pop=0)
            : curNode(n), popTimes(pop) {}
    };
    
    node* root;
    void clear(node*& target);
    node* find(const T& dt) const;
public:
    binTree();
    binTree(const T& dt);
    ~binTree();
    void createFromStd(const T& emptyFlag);
    
    void clear();
    bool isempty() const;
    T Root(const T& emptyFlag) const;
    T father(const T& dt, const T& emptyFlag) const;
    T leftChild(const T& dt, const T& emptyFlag) const;
    T rightChild(const T& dt, const T& emptyFlag) const;
    void rmLeftChild(const T& dt);
    void rmRightChild(const T& dt);
    void preOrdTrav() const;
    void midOrdTrav() const;
    void postOrdTrav() const;
    void levelTrav() const;
    
    // 常见实现
    int size() const;
};

template <class T>
binTree<T>::binTree() { root = nullptr; }

template <class T>
binTree<T>::binTree(const T& dt) { root = new node(dt); }

template <class T>
binTree<T>::~binTree() { clear(root); }

template <class T>
void binTree<T>::createFromStd(const T& emptyFlag) {
    seqQueue<node*> tasks;
    T left, right;
    if (!root) { 
        std::cout << "root: "; std::cin >> left;
        if (left != emptyFlag) tasks.enQueue(root = new node(left));
    } else { tasks.enQueue(root); }
    while (!tasks.isempty()) {
        node* cur = tasks.deQueue();
        std::cout << "the left child & the right child of " << cur->data << ": ";
        std::cin >> left >> right;
        if (left != emptyFlag)
            tasks.enQueue(cur->left = new node(left));
        if (right != emptyFlag)
            tasks.enQueue(cur->right = new node(right));
    }
}

template <class T>
bool binTree<T>::isempty() const { return root == nullptr; }

template <class T>
void binTree<T>::clear() { clear(root); root = nullptr; }

template <class T>
T binTree<T>::Root(const T& emptyFlag) {
    if (root == nullptr) return emptyFlag;
    return root->data;
}

template <class T>
T binTree<T>::father(const T& dt, const T& emptyFlag) { return emptyFlag; }

template <class T>
T binTree<T>::leftChild(const T& dt, const T& emptyFlag) const {
    node* cur = find(dt);
    if (!cur || !(cur->left)) return emptyFlag;
    return cur->left->data;
}

template <class T>
T binTree<T>:: rightChild(const T& dt, const T& emptyFlag) const {
    node* cur = find(dt);
    if (!cur || !(cur->right)) return emptyFlag;
    return cur->right->data;
}

template <class T>
void binTree<T>::rmLeftChild(const T& dt) { 
    node* cur = find(dt);
    if (!cur || !(cur->left)) return;
    clear(cur->left);
}

template <class T>
void binTree<T>::rmRightChild(const T& dt) { 
    node* cur = find(dt);
    if (!cur || !(cur->right)) return;
    clear(cur->right);
}

template <class T>
void binTree<T>::preOrdTrav() const {
    if (!root) return;
    seqStack<node*> tasks;
    tasks.push(root);
    while (!tasks.isempty()) {
        node* tmp = tasks.pop();
        std::cout << tmp->data << ' ';
        if (tmp->right) tasks.push(tmp->right);
        if (tmp->left) tasks.push(tmp->left);
    }
}

template <class T>
void binTree<T>::midOrdTrav() const {
    if (!root) return;
    seqStack<travNode> tasks;
    tasks.push(root);
    while (!tasks.isempty()) {
        travNode tmp = tasks.pop();
        if (tmp.popTimes == 0) {
            ++tmp.popTimes;
            tasks.push(tmp);
            if (tmp.curNode->left)
                tasks.push(travNode(tmp.curNode->left));
        }
        else {
            std::cout << tmp.curNode->data << ' ';
            if (tmp.curNode->right)
                tasks.push(travNode(tmp.curNode->right));
        }
    }
}

template <class T>
void binTree<T>::postOrdTrav() const {
    if (!root) return;
    seqStack<travNode> tasks;
    tasks.push(root);
    while (!tasks.isempty()) {
        travNode tmp = tasks.pop();
        switch (tmp.popTimes) {
        case 0:
            ++tmp.popTimes;
            tasks.push(tmp);
            if (tmp.curNode->left)
                tasks.push(travNode(tmp.curNode->left));
            break;
        case 1:
            ++tmp.popTimes;
            tasks.push(tmp);
            if (tmp.curNode->right)
                tasks.push(travNode(tmp.curNode->right));
            break;
        default:
            std::cout << tmp.curNode->data << ' ';
        }
    }
}

template <class T>
void binTree<T>::levelTrav() const {
    if (!root) return;
    seqQueue<node*> tasksQ;
    tasksQ.enQueue(root);
    while (!tasksQ.isempty()) {
        node* tmp = tasksQ.deQueue();
        std::cout << tmp->data << ' ';
        if (tmp->left) tasksQ.enQueue(tmp->left);
        if (tmp->right) tasksQ.enQueue(tmp->right);
    }
}

template <class T>
int binTree<T>::size() const {
    if (!root) return 0;
    int ans = 0;
    seqStack<node*> tasks;
    tasks.push(root);
    while (!tasks.isempty()) {
        node* tmp = tasks.pop();
        if (tmp->left) tasks.push(tmp->left);
        if (tmp->right) tasks.push(tmp->right);
        ++ans;
    }
}

5.4 二叉线索树

在二叉树中利用空指针域，如果一个结点的左/右指针为空，就将某种遍历序列中的这个结点的直接前驱结点地址存在该位置，这种二叉树就叫线索树

对一棵中序线索树而言，中序遍历的非递归实现可以不使用栈；

5.5 哈夫曼树

哈夫曼树的存储方法
- 哈夫曼树只有度为2的结点和叶结点，总结点数=2*需编码字符数-1【元素数了解】
- 哈夫曼树建立后一般不会进行结点增删
所以采用规模数为2n的数组静态（顺序）存储

哈夫曼树的建立：哈夫曼算法

step1：从给定权值和数据的集合中构建一片只有根结点的二叉树森林；

将需编码数据和权值对应地加入第 n~2n-1 索引的数组内，其他位置所有数据置为0（第0索引空出）；
step2：执行 n-1 次循环，选择每次森林中权值最小、次最小的两棵树，以这两棵树为左右子树构建出一棵新树，移除这两棵树并将新树加入；

执行 n-1 次循环，第 i 次在下标 n + i - 1 到 2n - 1 之间寻找满足：父结点对应值为0（当前是树根）且权值最小和次小的结点，并且①在 n + i 的位置填入 {权值=两点权值和；左右子节点为找到的两结点} 的结点；②修改被找到的那两个结点的父结点为 $n+i$ ；

即：修改父子关系、置权归并；
step3：如果只剩下一个树，那么这个树根上的结点的值即为所求；

⚠易错警示：注意比较森林中的最小两个权的树，不一定是”最大的“那个树，切忌惯性思维；

// Huffman Tree
template <class T>
class hfTree {
private:
    struct hfNode {
        T data;
        int weight;
        int parent;
        int left;
        int right;
    };

    hfNode* treeData;
    // The length of the treeData(hfNode*)
    // = 2 * numOfData.
    int length;

public:
    struct hfCode{
        T data;
        std::string code;
    };
    hfTree(const T* dt, const int* w, int size);
    ~hfTree();
    void getCode(hfCode results[]) const;
};

template <class T>
hfTree<T>::hfTree(const T* dt, const int* w, int size) {
    length = size * 2;
    treeData = new hfNode[length];
    for (int i = size; i < length; ++i) {
        treeData[i].data = dt[i - size];
        treeData[i].weight = w[i - size];
        treeData[i].parent = treeData[i].left = treeData[i].right = 0;
    }
    // 想要提高这一段速度，可以把这个 O(n^2) 代码改成优先级队列的操作
    for (int i = size - 1; i > 0; --i) {
        int min_1, min_2, min_1_idx = 0, min_2_idx = 0;
        min_1 = min_2 = INT32_MAX;
        for (int j = i + 1; j < length; ++j) {
            if (treeData[j].parent == 0) {	// The root of the subtree.
                if (treeData[j].weight < min_1) {
                    min_2 = min_1;			// Give the last value of min_1 to min_2
                    min_1 = treeData[j].weight;	// so that min_2 can be the second smallest element.
                    min_2_idx = min_1_idx;
                    min_1_idx = j;
                }
                else if (treeData[j].weight < min_2) {
                    min_2 = treeData[j].weight;
                    min_2_idx = j;
                }
            }
        }
        // The end of this round. Change the hier-info & weight.
        treeData[i].parent = 0;
        treeData[i].weight = min_1 + min_2;
        treeData[i].left = min_1_idx;
        treeData[i].right = min_2_idx;
        treeData[min_1_idx].parent = i;
        treeData[min_2_idx].parent = i;
    }
}

template <class T>
hfTree<T>::~hfTree() {
    if (treeData) delete[] treeData;
}

template <class T>
void hfTree<T>::getCode(hfCode result[]) const {
    int size = length / 2;
    for (int i = size; i < length; ++i) {
        int step = i;
        result[i - size].data = treeData[i].data;
        result[i - size].code = "";
        while (step > 0) {
            result[i - size].code = (
                treeData[treeData[step].parent].left==step
                ? "0" : "1"
            ) + result[i - size].code;
            step = treeData[step].parent;
        }
    }
}

哈夫曼树的重要相关概念
- 结点的带权路径长 = 路径权值 * 路径长（=深度-1）；
- 树的带权路径长 = 所有叶结点的带权路径之和；
哈夫曼编码求解的时间复杂度分析
- 树高根据情况在：$O(log_2n)\sim O(n)$ 规模，循环查找所有编码，故复杂度在 $O(nlog_2n)\sim O(n^2)$ 之间；

5.6 二叉树、树与森林的转换

树的存储实现
- 孩子链表示法：静态孩子链表（表头数组存储所有结点，会指向下标链表）、动态孩子链表（所有结点组成一个链表）；
  
  可以考虑增加一个结点字段存放父结点，称“带双亲的孩子链表示法”
- 孩子兄弟链表示法（最常用）：左指针指向第一个儿子 | 数据 | 右指针指向第一个兄弟（不重复）
  
  转换成二叉树后，根结点一定没有右儿子；
- 双亲表示法：通过指向父结点的指针将树中结点关联（不相交集可以用此方法存储）；
森林的存储实现：每棵树孩子兄弟链 + 右子树拼接；
树的遍历：前序、后序、层次；

Chapter 6 优先级队列

优先级队列不宜借助线性结构实现，因为出队 / 入队一定有一个效率为 O(n)；

6.1 重要概念集合

二叉堆：一棵满足结构性、有序性的二叉树（完全二叉树）；
二叉堆结构性优势：树高度尽可能小，可以采用顺序存储，最坏对数级别时间复杂度；
二叉堆有序性优势：算法上保证入队、出队的时间性能；
优先级队列的基本运算：同队列；

6.2 优先级队列的实现方法：树形结构

存储实现：二叉堆【队长度、队容量、二叉堆根结点】

⚠ATTENTION：

如果二叉堆（完全二叉树）存储在数组中，规定0号位不放元素，那么可以用之前完全二叉树的结论：i 号位的左儿子 2i、右儿子 2i+1、父结点 floor(i/2)（如果有的话）；

但如果二叉堆规定0号位放元素，那么需要转换一下：左儿子2i+1、右儿子2i+2、父结点floor((i-1)/2)；

推导：左子结点映射：i -> 2i，索引移动后，i - 1 -> 2i - 1；现在只知道 i - 1的结点的左子结点对应 2i - 1，想要知道 i 的左子结点，需要整体换元：i -> 2(i + 1)-1 = 2i+1；其他同理;

template <class T>
class priorityQueue {
private:
    T* data;
    int maxSize;
    int length;
    void doubleSpace();
    // 可复用：使从第n号元素开始的以下结点全部平衡
    void percolateDown(int n);
public:
    priorityQueue(int capacity=10);
    priorityQueue(T* sequence, int size);
    ~priorityQueue();
    void enQueue(const T& dt);
    T deQueue();
    T getHead() const;
    bool isempty() const;
};

运算实现（以使用0号元素的、最小化堆【可以添加comp模板参数以实现自定义最大/最小化堆】实现优先级队列为例）

[PRIVATE] 扩容操作：完全与线性表相同

template <class T>
void priorityQueue<T>::doubleSpace() {
    T* tmp = data;
    data = new T[2 * maxSize];
    for (int i = 0; i < maxSize; ++i)
        data[i] = tmp[i];
    delete[] tmp; maxSize *= 2;
}

创建、删除 $O(1)$：分配数组、设置队长和容量；释放空间；

template <class T>
priorityQueue<T>::priorityQueue(int capacity) {
    maxSize = capacity; length = 0;
    data = new T[capacity];
}

template <class T>
priorityQueue<T>::~priorityQueue() { if (data) delete[] data; }

读头、判空 $O(1)$

template <class T>
bool priorityQueue<T>::isempty() const { return length == 0; }

template <class T>
T priorityQueue<T>::getHead() const {
    if (length == 0) throw noElementException();
    return data[0];
}

入队操作：注意：$平均\space O(1)、最差\space O(log_2n)$

采用向上过滤法，入队到末尾，检查父结点和当前结点是否违反有序性，若是，交换并继续检查；若否，插入完成；

template <class T>
void priorityQueue<T>::enQueue(const T& dt) {
    if (length == maxSize) doubleSpace();
    int idx = length;
    while (idx > 0) {
        if (data[(idx - 1) / 2] > dt)
            data[idx] = data[(idx - 1) / 2];
        idx = (idx - 1) / 2;
    }
    data[length++] = dt;
}

[PRIVATE] 平衡操作：注意：$平均、最坏均为\space O(log_2n)$

向下过滤，保证 n 号结点以下的所有部分满足有序性；

template <class T>
void priorityQueue<T>::percolateDown(int n) {
    T tmp = data[n]; int next;
    while (2 * n + 1 < length) {
        next = 2 * n + 1;
        if (next + 1 < length && data[next] > data[next + 1]) ++next;
        if (tmp > data[next]) data[n] = data[next];
        n = next;
    }
    data[n] = tmp;
}

出队操作：注意：$平均、最坏均为\space O(log_2n)$

采用向下过滤法，将尾部元素覆盖到根结点上（为了保持堆的有序性，但同时也造成平均时间复杂度没有办法保持在线性级别），并percolateDown使得根结点以下处于平衡状态

template <class T>
T priorityQueue<T>::deQueue() {
    if (length == 0) throw noElementException();
    T ans = data[0];
    data[0] = data[--length];
    percolateDown(0);
    return ans;
}

整体创建操作：注意：$平均、最坏均为\space O(n)$，证明：$S=\sum\limits_{i=1}^h{2^{i-1}(h-i)}=N-h$

不用n次入队的方法；转换问题，为了避免递归从逆层次（最后一个非叶节点开始）向上进行平衡操作，类似动态规划，使得遍历到顶时整个列表由“完全二叉树”变为二叉堆；

template <class T>
priorityQueue<T>::priorityQueue(T* sequence, int size) {
    maxSize = size + 10; length = size;
    data = new T[size + 10];
    for (int i = 0; i < size; ++i)
        data[i] = sequence[i];
    // Build the heap.
    for (int i = length / 2 - 1; i >= 0; --i)
        percolateDown(i);
}

6.3 D堆、可归并堆（左堆、斜堆、二项堆）

略，在高级数据结构中详细叙述

6.4 优先级队列的应用

多柜台排队系统

原理是：创建一个事件优先级队列，和一个普通的等待队列；先生成所有人的到达时间进队，再逐个出队，检查事件类型：是离开类型，则检查等待队列

创建一个事件优先级队列epQueue
创建一个等待队列wQueue
时间置为0
for (循环customerNum次) {
    按指数分布（伪随机）生成顾客到达事件时间间隔dt
    将到达事件（上一事件时间+dt）入队epQueue
}
while (epQueue非空) {
    epQueue队头出队
    设置当前时间为事件时间
    if (事件类型是到达) {
        if (空闲柜台数 > 0) {
            --空闲柜台数
            生成所需服务时间st
            将事件类型设置为离开
            将事件时间+st
            入队epQueue
        }
        else 事件入队wQueue
    }
    else {
        if (等待队列非空) {
            wQueue队头出队
            统计等待时间
            生成服务所需时间st
            将事件类型设置为离开
            将事件时间+st
            入队epQueue
        }
        else ++空闲柜台数
    }
}
计算平均等待时间ave_t